Abstract
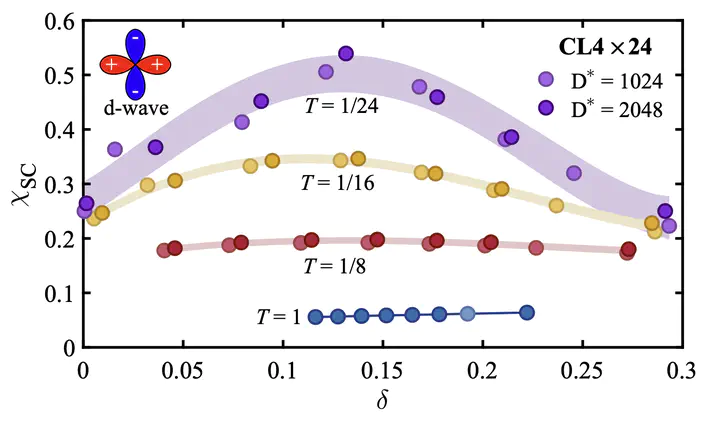
Accurate simulations of the two-dimensional (2D) Hubbard model constitute one of the most challenging problems in condensed matter and quantum physics. Here we develop a tangent space tensor renormalization group (tanTRG) approach for the calculations of the 2D Hubbard model at finite temperature. An optimal evolution of the density operator is achieved in tanTRG with a mild $O(D^3)$ complexity, where the bond dimension $D$ controls the accuracy. With the tanTRG approach we boost the low-temperature calculations of large-scale 2D Hubbard systems on up to a width-8 cylinder and $10 imes10$ square lattice. For the half-filled Hubbard model, the obtained results are in excellent agreement with those of determinant quantum Monte Carlo (DQMC). Moreover, tanTRG can be used to explore the low-temperature, finite-doping regime inaccessible for DQMC. The calculated charge compressibility and Matsubara Green’s function are found to reflect the strange metal and pseudogap behaviors, respectively. The superconductive pairing susceptibility is computed down to a low temperature of approximately $1/24$ of the hopping energy, where we find $d$-wave pairing responses are most significant near the optimal doping. Equipped with the tangent-space technique, tanTRG constitutes a well-controlled, highly efficient and accurate tensor network method for strongly correlated 2D lattice models at finite temperature.